归并排序(Merge Sort)

归并排序介绍

根据具体的实现，归并排序包括"从上往下"和"从下往上"2种方式。

归并排序动态图

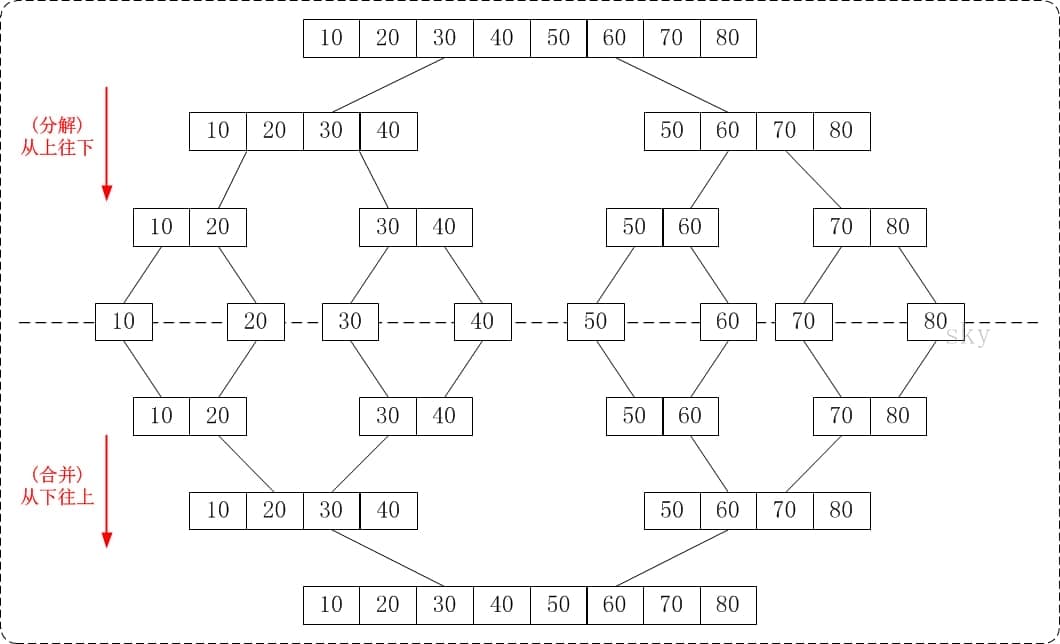
从下往上的归并排序

将待排序的数列分成若干个长度为1的子数列，然后将这些数列两两合并；得到若干个长度为2的有序数列，再将这些数列两两合并；得到若干个长度为4的有序数列，再将它们两两合并；直接合并成一个数列为止。这样就得到了我们想要的排序结果。(参考下面的图片)

从上往下的归并排序

它与"从下往上"在排序上是反方向的。它基本包括3步：

• 分解 -- 将当前区间一分为二，即求分裂点 mid = (low + high)/2;

• 求解 -- 递归地对两个子区间a[low...mid] 和 a[mid+1...high]进行归并排序。递归的终结条件是子区间长度为1。

• 合并 -- 将已排序的两个子区间a[low...mid]和 a[mid+1...high]归并为一个有序的区间a[low...high]。

归并排序实现

从上往下的归并排序

从上往下的归并排序采用了递归的方式实现。它的原理非常简单，如下图:

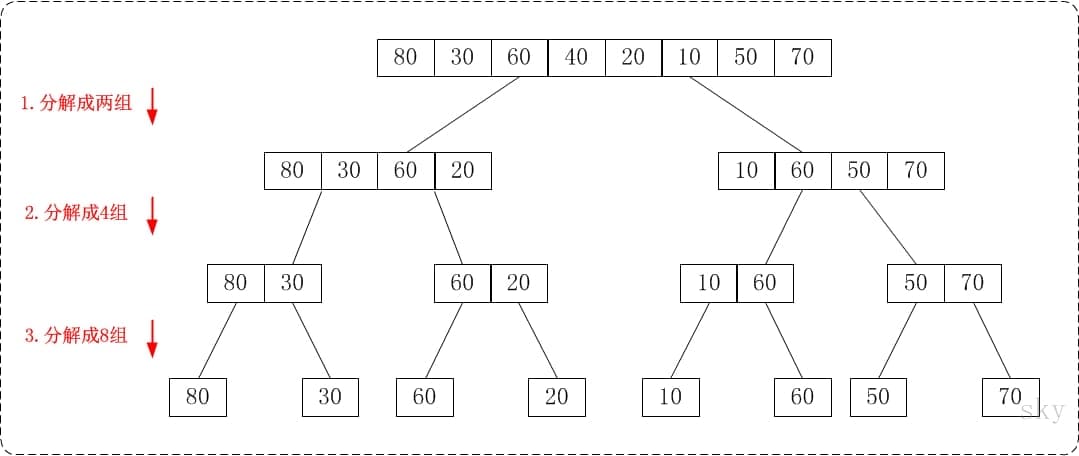
通过"从上往下的归并排序"来对数组{80,30,60,40,20,10,50,70}进行排序时:

• 将数组{80,30,60,40,20,10,50,70}看作由两个有序的子数组{80,30,60,40}和{20,10,50,70}组成。对两个有序子树组进行排序即可。

• 将子数组{80,30,60,40}看作由两个有序的子数组{80,30}和{60,40}组成。

  • 将子数组{20,10,50,70}看作由两个有序的子数组{20,10}和{50,70}组成。

• 将子数组{80,30}看作由两个有序的子数组{80}和{30}组成。

  • 将子数组{60,40}看作由两个有序的子数组{60}和{40}组成。
  • 将子数组{20,10}看作由两个有序的子数组{20}和{10}组成。
  • 将子数组{50,70}看作由两个有序的子数组{50}和{70}组成。

从下往上的归并排序

从下往上的归并排序的思想正好与"从下往上的归并排序"相反。如下图:

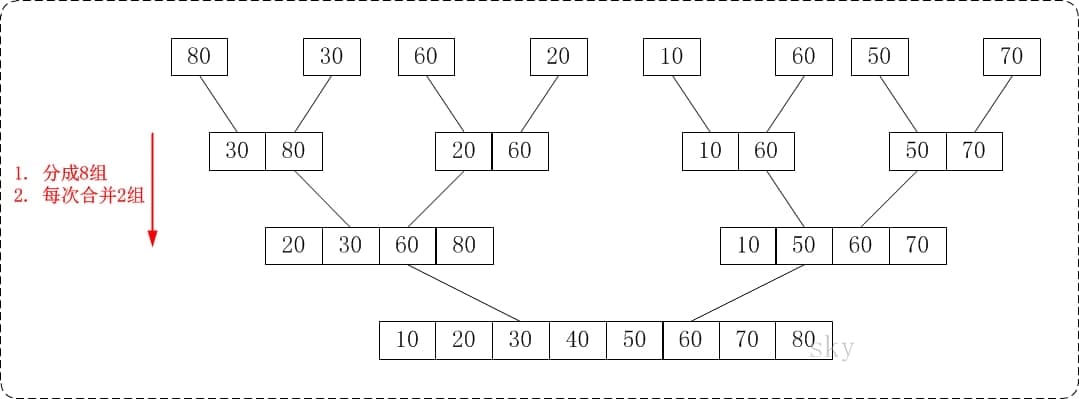
通过"从下往上的归并排序"来对数组{80,30,60,40,20,10,50,70}进行排序时:

• 将数组{80,30,60,40,20,10,50,70}看作由8个有序的子数组{80},{30},{60},{40},{20},{10},{50}和{70}组成。
• 将这8个有序的子数列两两合并。得到4个有序的子树列{30,80},{40,60},{10,20}和{50,70}。
• 将这4个有序的子数列两两合并。得到2个有序的子树列{30,40,60,80}和{10,20,50,70}。
• 将这2个有序的子数列两两合并。得到1个有序的子树列{10,20,30,40,50,60,70,80}。

归并排序的时间复杂度和稳定性

归并排序时间复杂度

归并排序的时间复杂度是O(N*lgN)。

假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢? 归并排序的形式就是一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的可以得出它的时间复杂度是O(N*lgN)。

归并排序稳定性

归并排序是稳定的算法，它满足稳定算法的定义。

算法稳定性 -- 假设在数列中存在a[i]=a[j]，若在排序之前，a[i]在a[j]前面；并且排序之后，a[i]仍然在a[j]前面。则这个排序算法是稳定的！

代码实现

/**
 * @description：归并排序
 * @author：SunXiaoMin
 * @create：2022-11-30
 * @Version：
 */
public class MergeSort {
    /**
     * 将一个数组中的两个相邻有序区间合并成一个
     * <p>
     * 参数说明:
     * a -- 包含两个有序区间的数组
     * start -- 第1个有序区间的起始地址。
     * mid   -- 第1个有序区间的结束地址。也是第2个有序区间的起始地址。
     * end   -- 第2个有序区间的结束地址。
     */
    public static void merge(int[] a, int start, int mid, int end) {
        // tmp是汇总2个有序区的临时区域
        int[] tmp = new int[end - start + 1];
        // 第1个有序区的索引
        int i = start;
        // 第2个有序区的索引
        int j = mid + 1;
        // 临时区域的索引
        int k = 0;

        while (i <= mid && j <= end) {
            if (a[i] <= a[j]) {
                tmp[k++] = a[i++];
            } else {
                tmp[k++] = a[j++];
            }
        }

        while (i <= mid) {
            tmp[k++] = a[i++];
        }

        while (j <= end) {
            tmp[k++] = a[j++];
        }
        // 将排序后的元素，全部都整合到数组a中。
        for (i = 0; i < k; i++) {
            a[start + i] = tmp[i];
        }
        tmp = null;
    }

    /**
     * 归并排序(从上往下)
     * <p>
     * 参数说明:
     * a -- 待排序的数组
     * start -- 数组的起始地址
     * endi -- 数组的结束地址
     */
    public static void mergeSortUp2Down(int[] a, int start, int end) {
        if (a == null || start >= end) {
            return;
        }
        int mid = (end + start) / 2;
        // 递归排序a[start...mid]
        mergeSortUp2Down(a, start, mid);
        // 递归排序a[mid+1...end]
        mergeSortUp2Down(a, mid + 1, end);

        // a[start...mid] 和 a[mid...end]是两个有序空间，
        // 将它们排序成一个有序空间a[start...end]
        merge(a, start, mid, end);
    }


    /**
     * 对数组a做若干次合并: 数组a的总长度为len，将它分为若干个长度为gap的子数组；
     * 将"每2个相邻的子数组" 进行合并排序。
     * <p>
     * 参数说明:
     * a -- 待排序的数组
     * len -- 数组的长度
     * gap -- 子数组的长度
     */
    public static void mergeGroups(int[] a, int len, int gap) {
        int i;
        // 两个相邻的子数组的长度
        int twolen = 2 * gap;

        // 将"每2个相邻的子数组" 进行合并排序。
        for (i = 0; i + 2 * gap - 1 < len; i += (2 * gap)) {
            merge(a, i, i + gap - 1, i + 2 * gap - 1);
        }

        // 若 i+gap-1 < len-1，则剩余一个子数组没有配对。
        // 将该子数组合并到已排序的数组中。
        if (i + gap - 1 < len - 1) {
            merge(a, i, i + gap - 1, len - 1);
        }
    }

    /**
     * 归并排序(从下往上)
     * <p>
     * 参数说明:
     * a -- 待排序的数组
     */
    public static void mergeSortDown2Up(int[] a) {
        if (a == null) {
            return;
        }

        for (int n = 1; n < a.length; n *= 2) {
            mergeGroups(a, a.length, n);
        }
    }

    public static void main(String[] args) {
        int i;
        int a[] = {80, 30, 60, 40, 20, 10, 50, 70};

        System.out.printf("before sort:");
        for (i = 0; i < a.length; i++) {
            System.out.printf("%d ", a[i]);
        }
        System.out.printf("\n");


        // 归并排序(从上往下)
//        mergeSortUp2Down(a, 0, a.length - 1);
        // 归并排序(从下往上)
        mergeSortDown2Up(a);


        System.out.printf("after  sort:");
        for (i = 0; i < a.length; i++) {
            System.out.printf("%d ", a[i]);
        }
        System.out.printf("\n");
    }
}