选择排序(Selection sort)

选择排序介绍

它的基本思想是: 首先在未排序的数列中找到最小(or最大)元素，然后将其存放到数列的起始位置；接着，再从剩余未排序的元素中继续寻找最小(or最大)元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

选择排序动态图

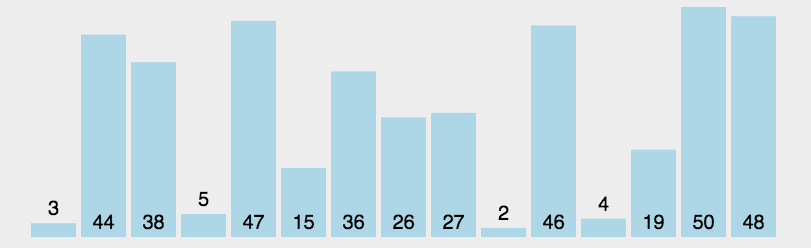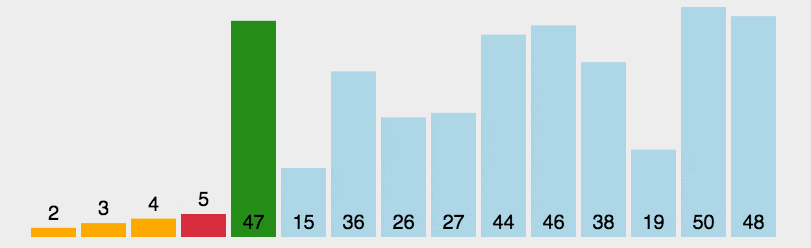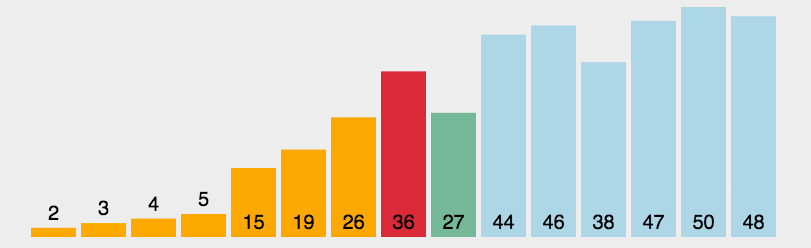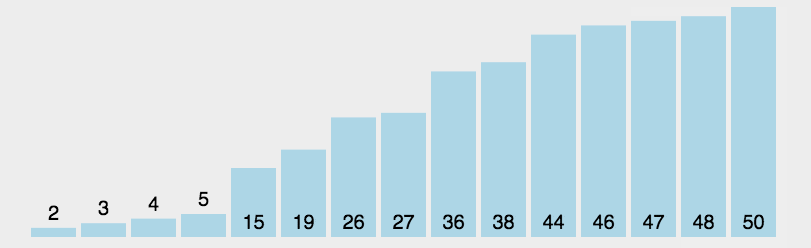
选择排序实现

下面以数列{20,40,30,10,60,50}为例，演示它的选择排序过程(如下图)。

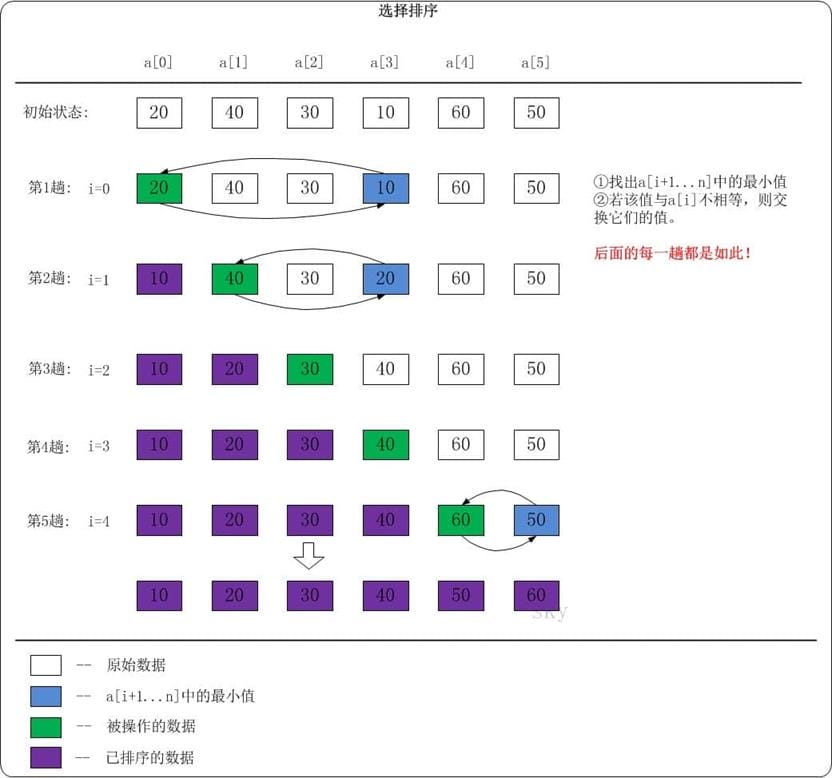
排序流程

• 第1趟: i=0。找出a[1...5]中的最小值a[3]=10，然后将a[0]和a[3]互换。 数列变化: 20,40,30,10,60,50 -- > 10,40,30,20,60,50

• 第2趟: i=1。找出a[2...5]中的最小值a[3]=20，然后将a[1]和a[3]互换。 数列变化: 10,40,30,20,60,50 -- > 10,20,30,40,60,50

• 第3趟: i=2。找出a[3...5]中的最小值，由于该最小值大于a[2]，该趟不做任何处理。

• 第4趟: i=3。找出a[4...5]中的最小值，由于该最小值大于a[3]，该趟不做任何处理。

• 第5趟: i=4。交换a[4]和a[5]的数据。 数列变化: 10,20,30,40,60,50 -- > 10,20,30,40,50,60

选择排序的时间复杂度和稳定性

选择排序时间复杂度

选择排序的时间复杂度是O(N2)。

假设被排序的数列中有N个数。遍历一趟的时间复杂度是O(N)，需要遍历多少次呢? N-1！因此，选择排序的时间复杂度是O(N2).

选择排序稳定性

选择排序的稳定性是有一些争议的，不过一般提到排序算法，往往默认是数组实现，所以通常认为选择排序是不稳定的。知乎上有个讨论可以看下。

• 回顾：什么是排序算法的稳定性？
  • 假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
• 数组实现和链表实现的差异
  • 用数组实现的选择排序是不稳定的，用链表实现的选择排序是稳定的。
  • 不过，一般提到排序算法时，大家往往会默认是数组实现，所以选择排序是不稳定的。
• 此外，排序算法的稳定性也是可以改变的，只是需要额外的时间和空间
  • 有很多办法可以将任意排序算法变成稳定的，但是，往往需要额外的时间或者空间；而我们默认情况谈算法的稳定性是不考虑这种实现的。

代码实现

/**
 * @description：选择排序
 * @author：SunXiaoMin
 * @create：2022-11-30
 * @Version：
 */
public class SelectSort {
    /**
     * 选择排序
     * <p>
     * 参数说明:
     * a -- 待排序的数组
     * n -- 数组的长度
     */
    public static void selectSort(int[] a, int n) {
        int i;        // 有序区的末尾位置
        int j;        // 无序区的起始位置
        int min;    // 无序区中最小元素位置

        for (i = 0; i < n; i++) {
            min = i;

            // 找出"a[i+1] ... a[n]"之间的最小元素，并赋值给min。
            for (j = i + 1; j < n; j++) {
                if (a[j] < a[min]) {
                    min = j;
                }
            }

            // 若min!=i，则交换 a[i] 和 a[min]。
            // 交换之后，保证了a[0] ... a[i] 之间的元素是有序的。
            if (min != i) {
                int tmp = a[i];
                a[i] = a[min];
                a[min] = tmp;
            }
        }
    }

    public static void main(String[] args) {
        int i;
        int[] a = {20, 40, 30, 10, 60, 50};

        System.out.printf("before sort:");
        for (i = 0; i < a.length; i++) {
            System.out.printf("%d ", a[i]);
        }
        System.out.printf("\n");


        selectSort(a, a.length);


        System.out.printf("after  sort:");
        for (i = 0; i < a.length; i++) {
            System.out.printf("%d ", a[i]);
        }
        System.out.printf("\n");
    }
}